Predicción de la Volatilidad de los Precios del Petróleo Mexicano: CGARCH Asimétrico con Distribuciones Normal y Laplace

Predicting Price Volatility of Mexican Petroleum: Asymmetric CGARCH with Normal and Laplace Distributions

Raúl de Jesús Gutiérrez*, Edgar Ortiz.**

Resumen

Uno de los problemas asociados con las exportaciones petroleras es la volatilidad de sus precios cuyo comportamiento se ha caracterizado por grandes desplomes en las últimas décadas. Este comportamiento se ha convertido en un crucial factor determinando la inestabilidad y falta de crecimiento económico de países emergentes cuyos ingresos dependen sustancialmente de sus ingresos petroleros. Este es el caso de México. Este trabajo predice la volatilidad de de los rendimientos de los precios de los petróleos mexicanos de exportación Maya e Istmo aplicando un modelo GARCH extendido y dos supuestos de distribución condicional durante el perído1989 a 2012. Los resultados se someten a la prueba estadística de Diebold-Mariano.

Palabras clave: Petróleo crudo, Predicción de la volatilidad, Distribución de Laplace, Prueba de Diebold-Mariano.

Abstract

One of the problems associated with oil exports is the price volatility, whose behavior was characterized by large crashes in recent decades. This behavior has become a crucial factor determining the instability and lack of economic growth in emerging countries whose incomes are substantially dependent on its oil revenues. This is the case of Mexico. This work predicts volatility of returns of prices of Mexican export petroleum Maya and Istmo applying an extended GARCH and two cases of conditional distribution during the period 1989 to 2012. The results were subjected to statistical Diebold-Mariano test.

Keywords: Crude Oil, Predicting volatility Laplace distribution, Diebold-Mariano test.

Clasificación JEL: Q40, C32, C52, E30.

* Dr. Raúl de Jesús Gutiérrez. Facultad de Economía. Universidad Autónoma del Estado de México.

** Dr. Edgar Ortiz. Facultad de Ciencias Políticas y Sociales Universidad Nacional Autónoma de México

Artículo Recibido: 15 de febrero del 2014 Artículo Aceptado: 25 de abril de 2014

1. Importancia de la volatilidad internacional de los precios del petróleo

La apertura económico-financiera implementada por muchos países a fin de fomentar su competitividad al igual que la penetración de sus productos a los mercados internacionales no ha sido del todo benéfica para el caso de las economías emergentes exportadoras de materias primas. Sus exportaciones han estado sujetas a frecuentes turbulencias que han desestabilizado sus ingresos lo que a su vez ha sido el mecanismo de contagio para generar crisis generalizadas de sus economías. Esta situación, desafortunadamente se ha convertido en un ciclo recurrente; eventos de carácter climático, capacidad de refinería y acuerdos institucionales internacionales para recortar la producción global han transformado el equilibrio económico a nivel mundial. Sin embargo, no solo el comportamiento cíclico desfavorable de los precios de las materias primas ha sido “causante” de la desproporcionada inestabilidad y falta de crecimiento de estos países. Causa fundamental ha sido la incapacidad de sus gobiernos para formular políticas alternativas de crecimiento para sus economías. Particularmente los países en vías de desarrollo exportadores de petróleo han desarrollado una dependencia persistente en el comportamiento de los precios de petróleo internacionales: la bonanza económica caracteriza sus economías si los precios del petróleo son altos y caracterizados por cierta estabilidad; sus economías se sumen en graves crisis como resultado de precios del petróleo desfavorable y volátil. Sus políticas económicas no han trascendido estas tendencias. En primer lugar es preciso que en estos países se modele y prediga el comportamiento de los precios internacionales del petróleo; en segundo lugar deben enfatizar, por ejemplo, políticas de innovación y creación tecnológica; esta es la respuesta idónea y de largo

a una economía de la innovación; si es preciso modelar y predecir la volatilidad de los precios internacionales del petróleo, muy especial para el caso de México que hacia el año 2050 apunta a ser la octava economía mundial.1

Recientemente, múltiples estudios ha analizado las características de la volatilidad dinámica a través de los tradicionales modelos ARCH y GARCH y sus variantes asumiendo innovaciones normales condicionales (Engle, 1982; Bollerslev, 1986; Kang et al., 2009). Sin embargo, la evidencia empírica ha demostrado que el patrón típico de las variaciones en los precios del petróleo es no estacionaria, más picuda alrededor de la media, altamente volátil, y caracterizado por colas pesadas. Así, solo reconociendo las características de leptocurtosis y del efecto de las colas pesadas es posible obtener estimar y predecir la volatilidad condicional con la mayor robustez estadística posible. La literatura sugiere la adopción de distribuciones de colas pesadas en la estructura GARCH. Entre las alternativas distribucionales propuestas, la distribución de errores generalizada, t-student simétrica y sesgada han sido empleadas para explicar las características no-normales de los rendimientos o innovaciones en el sector energético.

Otra alternativa a la distribución normal, y que no ha sido aplicada a los precios y rendimientos del petróleo, en particular en relación a los mercados de alto contenido de azufre se refiere a la distribución de Laplace, también conocida como distribución doble exponencial en la literatura económica-financiera. Esta distribución se caracteriza por tener colas más pesadas que la normal a pesar de carecer de un parámetro de forma específico o grados de libertad como en el caso de las distribuciones t-student y de errores generalizada.2 En conjunto con los modelos GARCH, el supuesto distribucional de Laplace ha

plazo para responder y aprovechar los retos de la

globalización caracterizada por ser una sociedad del conocimiento y de la información y del desarrollo tecnológico. Así, la estabilidad económica de estos países es un paso obligatorio para fomentar su paso

1 PWC, The World in 2050. The BRICs and Beyond: Prospects, Cha- llenges and Opportunities. 2013. Estimaciones del PIB en términos de paridad del poder adquisitivo.

2 La distribución de Laplace es un caso particular de la distribución hiperbólica cuando la curtosis es igual a 6. Para más detalles, véase Bibby y Sorensen (2003).

sido utilizado en la modelación de la naturaleza de las colas de la distribución de rendimientos para los índices S&P500, Nikkei 225 y S&P/TSX3 (Granger y Ding, 1995; Mittnik et al., 1998; Baker et al., 2008).

En cuanto a la estimación y predicción de la volatilidad cabe resaltar un problema de los modelos GARCH tradicionales: la presencia de diferentes grados de persistencia o memoria larga. Este hecho afecta la eficiencia de la estimación y predicción de la volatilidad en los precios del petróleo crudo ya que afecta los niveles en la estructura de la volatilidad condicional, atribuido a que los choques en el mercado tienden a desaparecer a una tasa hiperbólica, la cual es más lenta que el decaimiento exponencial de los choques en los modelos GARCH simétricos y asimétricos que analizan la dinámica de la volatilidad en el corto plazo (Baillie et al., 1996). Adicionalmente, es importante considerar que la presencia de persistencia es un factor fundamental en diversas aplicaciones financieras, particularmente en la medición del riesgo en el contexto del VaR, la selección de portafolios de inversión, en el diseño de estrategias de cobertura y la valuación de activos y opciones, dada su fuerte relación con la predictibilidad de la volatilidad condicional.

No obstante la investigación relacionada con la predicción de la volatilidad del petróleo es limitada. El presente trabajo contribuye a sobreponer tal restricción. En primer lugar, identifica las características empíricas comunes de la volatilidad de los rendimientos del petróleo, introduciendo una descomposición en su estructura para distinguir los efectos en los componentes de corto y largo plazos a través de un modelo CGARCH asimétrico o de dos componentes (ACGARCH), adoptando dos diferentes distribuciones condicionales para las innovaciones: normal y de Laplace. En segundo lugar, utiliza los precios diarios de dos tipos de petróleo mexicano (Maya e Istmo) para el análisis de la dinámica de la volatilidad cubriendo el periodo del 2 de enero de1989 al 31 de diciembre de 2012. En tercer lugar, para

3 Indice accionario de la Bolsa de Toronto.

el análisis de la evaluación de la capacidad predictiva de los modelos CGARCH asimétricos bajo los diferentes supuestos distribucionales, se comparan a una familia de modelos GARCH (estándar, EGARCH, GARCH-GJR, APARCH y

CGARCH simétrico) utilizando tres funciones de pérdidas robustas para diferentes periodos de predicción que van de 1, 5 y 20 días. Asimismo, la validación de la significancia estadística de la predicción óptima del modelo benchmark se lleva a cabo mediante la prueba de Diebold y Mariano (1995), utilizando el periodo del 2 de enero de 2008 al 31 de diciembre de 2012. Cabe resaltar que este periodo es relevante para el análisis de la predicción óptima de la volatilidad fuera de la muestra, dado que incluye a eventos importantes como la gran recesión de 2008-2009 originada por la crisis hipotecaria subprime y la crisis de deuda soberana de la zona euro de 2010-2012.

2. Petróleo y la Economía Mexicana

México ha perdido importancia como exportador de petróleo. Su posición mundial antes de la presente década siempre se encontraba entre los primeros diez lugares. Actualmente, como se indica en el Cuadro 1, se ubica en la posición 16, exportando en 1912 un promedio 1,511,000 barriles de crudo por día, una posición distante del primer lugar perteneciente a Arabia Saudita país que exporta 7,635,000 barriles de petróleo por día. Esta caída está relacionada con una notable baja en su producción petrolera, aunado a una sensible baja en sus reservas, profundizando su débil competitividad pues su petróleo se caracteriza por un alto contenido de azufre. Según Petróleos Mexicanos la producción de crudo llegó desde 1997 a un pico de 3, 333,000 barriles diarios en 2005; desde entonces ha seguido un patrón decreciente culminando en 2012 con 2,538 millones de barriles por día en 2012, una disminución de casi 24 por ciento.4 De acuerdo con las estadísticas de energía mundial

4 Pemex, Mexico’s Energy Reform & Pemex as a State Productive Enterprise. Pemex 2014. www.pemex.co.

de British Petroleum (2012), las reservas de México se estiman en 11.4 billones de barriles, mismas que han disminuido desde 1991 cuando alcanzaron los 50.9 billones de barriles, y que lo sitúan en el lugar 18 a nivel mundial por debajo de Brasil, China, Angola y Argelia.

El bajo desempeño de la economía en gran medida ha estado asociado con los decrecientes patrones en la producción y exportación de crudo. Desde su nacionalización en 1938, el petróleo ha jugado un papel clave en el crecimiento de la economía de México. Paradójicamente el auge en la producción y exportaciones petroleras iniciado en la década de 1970 fue prometedor; sin embargo esta palanca de desarrollo se baso en un alto precio del petróleo y un desproporcionado endeudamiento externo. La baja de los precios del petróleo a principios de la siguiente década y el alza en las tasas de interés internacionales terminaron con este esquema de desarrollo que no obstante no ha cambiado desde entonces. Así la industria petrolera continua jugando un papel clave en la economía. En el período 2001- 2011 la participación de las exportaciones petroleras y sus productos derivados en el Producto Interno Bruto se ha incrementado de 2.5 por ciento a 5.0 por ciento; los ingresos petroleros se han incrementado de US$ 13,231 a US56,385 millones de dólares. Sin embargo, la dependencia y vulnerabilidad de la economía del país se ha incrementado, primordialmente porque el presupuesto nacional depende de un 32 a un 35% de los excesivos impuestos cargados a la paraestatal. De hecho, la alta persistencia en la volatilidad es una de las típicas características en los precios del petróleo desde principios de la década de los noventa. Por lo que la adopción de modelos econométricos basados en procesos de innovaciones de colas pesadas es de vital importancia en la generación de información más completa de la estructura de la volatilidad, y que puede contribuir en el diseño de mejores políticas para reducir la incertidumbre y la exposición al riesgo en la economía nacional.5

5 La Reforma Energética aprobada en 2013 pretende sobreponer éstos problemas. No obstante, el futuro de la industria petrolera es incierto por lo que es preciso prevenir futuros riesgos identificando el comportamiento volátil de los precios del petróleo.

Cuadro 1

POSICIÓN (2012)	PAÍS	EXPORTACIONES (BARRILES/DÍA)
1	Arabia Saudita	7,635,000
2	Rusia	5,010,000
3	Irán	2,523,000
4	Emiratos Árabes Unidos	2,395,000
5	Noruega	2,184,000
6	Irak	2,170,000
7	Kuwait	2,127,000
8	Nigeria	2,102,000
9	Canadá	1,929,000
10	Estados Unidos	1,920,000
11	Venezuela	1,871,000
12	Países Bajos	1,871,000
13	Angola	1,851,000
14	Argelia	1,694,000
15	Libia	1,580,000
16	México	1,511,000
17	Kazajistán	1,390,000
18	Singapur	1,374,000
19	Reino Unido	1,311,000
20	Corea del Sur	1,100,000
21	Qatar	1,038,000
22	India	825,000
23	Brasil	801,200
24	Azerbaiyán	651,900
25	Malasia	644,900

Principales Países Exportadores de Petróleo Fuente: CIA World Fact Book, 2012.

3. Revisión de la Literatura

Múltiples estudios han analizado la dinámica de la volatilidad condicional a través de la estructura GARCH y sus variantes asumiendo el supuesto distribucional de innovaciones normales en los principales marcadores de referencia del petróleo (Sadorsky, 2006; Narayan y Narayan, 2007; Kang et al., 2009; Wei et al., 2010; Xu y Ouenniche, 2012). Varios investigadores han extendido los modelos GARCH bajo diferentes supuestos distribucionales para mejorar la modelación y predicción de la volatilidad. Salisu y Fasanya (2012) applican modelos simétricos GARCH y GARCH_M, así como modelos asimétricos TGARCH and EGARCH para predecir la volatilidad

de los precios de referencia del WTI oil; su estudio concluye que los modelos asimétricos son superiores. A su vez, Agnolucci (2009), comparara la capacidad predictiva de los modelos GARCH con la del modelo de volatilidad implícita obtenido al invertir la fórmula de forma cerrada de Black- Scholes; concluye que los modelos GARCH con distribución de errores generalizada proporciona un mejor desempeño para modelar y predecir la volatilidad de los futuros sobre el petróleo WTI.

Asimismo, analizando la capacidad de predicción óptima de una familia de modelos de volatilidad

-GARCH estándar, EGARCH, APARCH y FIGARCH-

con innovaciones t-student y evaluados bajo tres funciones de pérdidas, Cheong (2009) encontró evidencia, aunque no contundente, de que las especificaciones en la varianza condicional más simples y parsimoniosas presentan el mejor ajuste fuera de la muestra para el petróleo tipo Brent. Utilizando precios de contado semanales de 11 mercados internacionales de países exportadores e importadores de petróleo, cuatro funciones de pérdidas y pruebas estadísticas, Mohammadi y Su (2010) comparan el desempeño de 4 clases de modelos GARCH basados en la distribución de innovaciones t-student sesgada. Los resultados de la evaluación evidencian que los modelos EGARCH y APARCH son más apropiados para predecir la media y volatilidad condicional fuera de la muestra a diferencia de los modelos GARCH estándar e integrado fraccionariamente (FIGARCH). Por su parte, Marzo y Zagaglia (2010) estimaron tres modelos de volatilidad con diferentes supuestos distribucionales para las innovaciones de los rendimientos de los futuros sobre petróleo negociados en la Bolsa Mercantil de Nueva York. Los resultados del análisis fuera de la muestra sustentan que el modelo GARCH basado en la distribución de errores generalizada alcanza una excelente predicción óptima para los horizontes de 1 y 3 días, mientras que para horizontes de 5 y 15 días no existe modelo superior o inferior a los demás. En un trabajo más reciente que no requiere del conocimiento inicial de la distribución para describir las innovaciones en los rendimientos

del petróleo WTI y Brent, Hou y Suardi (2012) proponen un modelo GARCH no-paramétrico que mejora notablemente la capacidad predictiva fuera de la muestra con respecto a una extensa clase de modelos GARCH con innovaciones t-student, a pesar de que no especifican la característica de asimetría en el proceso de volatilidad. Finalmente, estimando un modelo EGARCH bajo régimen de volatilidad cambiaria y asumiendo que las innovaciones siguen una distribución t-student, Chang (2012) demostró que el impacto de los cambios de régimen y los efectos de la base asimétrica juegan un papel importante en la predicción de la volatilidad en los rendimientos de los futuros sobre el petróleo WTI.

4. Determinación y análisis básico de la muestra

4.1 Descripción de las series

Las características físicas y químicas del petróleo mexicano son importantes determinantes de sus precios en los mercados internacionales; esto es, es decir, de acuerdo a su densidad y contenido de azufre6 determinado por el parámetro internacional del Instituto Americano del Petróleo (API, por sus siglas en inglés). La producción de petróleo está compuesta por una canasta de crudos nacionales entre ellos se encuentra el pesado Maya con densidad de 22 grados API y contenido de azufre de 3.3%, el ligero Istmo con 33.6 grados API y 1.3% de azufre y el extra ligero Olmeca que alcanza una densidad de 39.3 grados y 0.8% de azufre en peso. La muestra del presente estudio para el análisis de la predicción de la volatilidad condicional, consiste de los precios diarios de los crudos Maya e Istmo para el periodo del 2 de enero de 1989 al 31 de diciembre de 2012, totalizando 6,228 observaciones. Las

6 El grado de densidad se puede clasificar de extra ligero a pesado, mientras que el contenido de azufre se caracteriza como dulce o ácido. En este sentido, los petróleos crudos con baja densidad y contenido de azufre son cotizados en los mercados internacionales a precios más altos que los pesados y corrosivos.

series de precios se obtuvieron de la base de datos de Bloomberg y la selección de la muestra fue de acuerdo a la disponibilidad de los datos.

4.2 Comportamiento de los precios del petróleo

La dinámica de los precios del petróleo nacional es ilustrada en la Gráfica 1. Durante el periodo 1989- 2012, los precios de contado oscilaron en un rango amplio entre $7.99 y $142.63 para el Istmo y entre

$5.80-$130.46 dólares por barril para el Maya. Aunque existen diferencias en la densidad y contenido de azufre en ambos tipos de petróleo, el comportamiento de los precios exhibe la misma tendencia a través del tiempo. De hecho, la naturaleza de los choques positivos y negativos en los precios de los crudos nacionales también ha sido estimulada por eventos económicos y políticos como en los mercados internacionales. Cabe resaltar, el estallido del conflicto en el Golfo Pérsico entre Kuwait e Irak en agosto de 1990, el cual generó incertidumbre en los precios del petróleo, pero la liberalización de Kuwait aunado a las políticas de uso racional de energía regresó la estabilidad a los mercados de energía en 1991-1997.

Gráfica 1. Comportamiento de los precios del

petróleo Maya e Istmo.

Otros eventos importantes que afectaron negativamente la tendencia de la cotización del petróleo Maya e Istmo fueron la tensión en Medio Oriente y la crisis asiática de 1997-1998. Sin embargo, desde el conflicto militar entre Estados Unidos e Irak en 2003, los precios de contado del petróleo jamás regresaron a los bajos niveles de 1998, e incluso en julio de 2008 registraron precios históricos de $130.46 y $142.63 dólares por barril, respectivamente. No obstante, este periodo de tendencia alcista en el precio del petróleo se vio interrumpido por el desplome espectacular a fines de diciembre de 2008, cuando descendieron a los niveles más bajos de $25.34 para el maya y $32.10 para el Istmo, precisamente en el momento cuando la economía global entró en un periodo de profunda recesión por la restricción del crédito. Pero una vez absorbido el efecto negativo de la recesión durante el 2009, otra tendencia alcista de largo plazo en el petróleo se observó en el periodo 2010-2012 cuando alcanzaron sus niveles más altos de $117.78 y $122.15 dólares por barril en febrero de 2012. Entre los factores importantes que explican esta alza en los energéticos, principalmente podemos mencionar los datos positivos en el mercado laboral de Estados Unidos y manufacturero en China, así

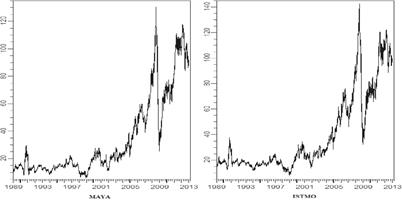
Fuente: Elaboración propia.

como la reducción de las tasas de interés para algunos países europeos. Sin olvidar, obviamente, los problemas en la oferta del hidrocarburo relacionados con el programa nuclear de Irán y los recortes en los niveles de producción de aproximadamente un millón de barriles diarios por parte de Siria, Sudán y Yemen. Sin embargo, la reducción en la demanda por la desaceleración económica global y los problemas financieros de Europa revirtió la tendencia alcista en ambos crudos nacionales a fines de junio, obligándolos a descender en promedio un 33% con respecto a los niveles máximos de 2012. Asimismo, la creciente amenaza del abismo fiscal de EEUU propicio que los precios del Maya ($85.95) e Istmo ($93.94) volvieran a descender en la tercera semana de noviembre de 2012, pero en esta ocasión el efecto fue rápidamente absorbido por los mercados internacionales.

Por otra parte, un hecho bien sabido es que los precios del petróleo se caracterizan por ser series no estacionarias, así que para fines del análisis empírico es importante transformar los precios a series estacionarias, calculando los rendimientos continuos a través de los cambios logarítmicos de

los precios de cierre de dos días consecutivos de operación; es decir:

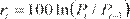
Las estadísticas básicas de los rendimientos para los dos tipos de petróleo se reportan en el Cuadro

2. Los rendimientos promedios son muy parecidos para ambas series; empero, la desviación estándar para los rendimientos del petróleo Maya es ligeramente más grande a la del Istmo. Además, las series de los rendimientos son negativamente sesgadas y exhiben exceso de curtosis para el periodo de estimación, esto es, propiedades de colas más anchas y largas que la distribución normal, particularmente la cola izquierda. El valor negativo del coeficiente sesgo revela que los rendimientos extremos negativos tienen mayor probabilidad de ocurrir que los rendimientos extremos positivos. 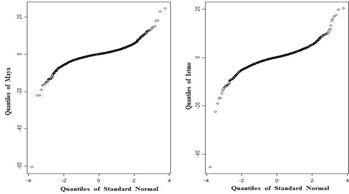Asimismo, el rechazo del supuesto de normalidad es confirmado por el valor del estadístico Jarque-Bera y la forma en “S” de la Gráfica 3 de los cuantiles de la distribución normal contra los cuantiles de las distribuciones empíricas para el petróleo Maya e Istmo, respectivamente.

Cuadro 2

Resultados de las estadísticas básicas de los rendimientos del petróleo

Petróleo	Media	Máximo	Mínimo	Desv.Est	Sesgo	Curtosis	JB	LM
Maya	0.0336	24.7652	-60.7012	2.8931	-1.5272	40.9751	373535	310.67(0)
Istmo	0.0303	20.3418	-45.3921	2.6261	-0.9702	23.1613	106439	315.32(0)

Nota: Las estadísticas básicas son expresadas en porcentajes para el periodo del 2 de enero de 1989 al 31 de diciembre de 2012. Desv. Est. representa la desviación estándar de los rendimientos. JB es el valor del estadístico Jarque-Bera de la prueba de normalidad y LM indica el valor del estadístico de la prueba del Multiplicador de Lagrange con valores-p entre paréntesis.

Gráfica 3. Gráfico cuantil-cuantil para los rendimientos del petróleo Maya e Istmo.

Fuente: Elaboración propia.

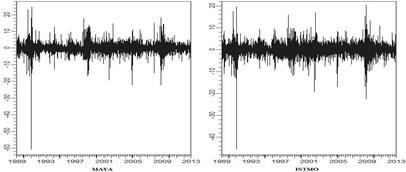
La Gráfica 2 que muestra la dinámica de los rendimientos para ambos tipos de petróleo a través del tiempo; se observa una fuerte evidencia de volatilidad en aglomeraciones; es decir, periodos de alta volatilidad seguido de periodos de relativa tranquilidad. Además, cabe resaltar que la intensidad del fenómeno de la heteroscedasticidad condicional es más pronunciada en los periodos de la guerra del Golfo Pérsico de 1991, la crisis asiática de 1997-1998, la recesión económica de los Estados Unidos en 2008-2009 y la crisis de deuda

soberana de la zona euro en 2010-2012, en donde los rendimientos experimentaron una sucesión de movimientos atípicos positivos y negativos en cortos intervalos de tiempo, en particular para el petróleo Maya. De hecho, la presencia de fuerte heteroscedasticidad o efectos ARCH en ambas series de rendimientos del petróleo se confirma por la significancia del estadístico de la prueba del Multiplicador de Lagrange a un nivel del 5% para 12 rezagos.

Gráfica 2. Dinámica de los rendimientos de los precios del petróleo Maya e Istmo.

Fuente: Elaboración propia.

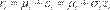
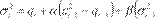En consecuencia, el análisis preliminar de los datos sugiere el uso de procesos GARCH y la incorporación de distribuciones de colas

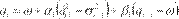pesadas en la modelación y predicción de la volatilidad condicional en las innovaciones de los

rendimientos del petróleo mexicano.

(1)

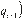(2)

(3)

5. Planteamiento de la Modelación Econométrica

5.1 Modelo GARCH de dos componentes

La dependencia de largo plazo o memoria larga observada en el proceso de la volatilidad ha sido documentada en una gran cantidad de estudios empíricos. Sin embargo es bien sabido que la propiedad de memoria larga no puede ser recogida por los modelos GARCH tradicionales, por lo que en la modelación se debe descomponer la volatilidad en dos componentes para describir el comportamiento de la persistencia en el corto y largo plazos.

Una especificación alternativa que puede capturar las propiedades de la memoria larga o alta persistencia en la serie de los rendimientos del petróleo, es el modelo CGARCH propuesto por Engle y Lee (1999). Esta aproximación permite descomponer la volatilidad condicional en dos componentes y analizar apropiadamente el comportamiento de decaimiento de la persistencia en la volatilidad en el corto y largo plazos que los modelos GARCH tradicionales (Christoffersen et al., 2006). El primer componente captura el impacto de las innovaciones en el corto plazo alimentado por los diversos eventos exógenos relacionados a aspectos económicos, geopolíticos, incluso de carácter especulativo, y que fluctúa en forma cíclica, mientras que el segundo componente recoge el impacto de largo plazo de las innovaciones esperadas.

La especificación del modelo CGARCH (1,1) se puede expresar de la siguiente forma:

Donde 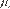representa la media condicional, indica las innovaciones en la ecuación de la media, el componente captura el nivel de la volatilidad en el largo plazo (tendencia), mismo que converge más lentamente al nivel de la volatilidad incondicional a una velocidad de

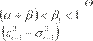. El error de predicción rezagado funciona como impulsor dinámico

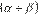para capturar el movimiento del componente de largo plazo dependiente del tiempo, mientras que la diferencia entre la varianza condicional y su volatilidad de largo plazo previa indica el componente de corto plazo de la varianza condicional, el cual converge a cero a una velocidad . De esta manera, la volatilidad condicional de largo plazo contrala las predicciones de la varianza condicional en la medida que el horizonte de predicción se incrementa.

En este marco, el modelo CGARCH proporciona una alternativa apropiada para recoger los efectos de corto y largo de la persistencia dinámica en la volatilidad condicional. Sin embargo, su potencial se reduce ante la presencia de efectos de apalancamiento o asimétricos porque es casi posible que los choques negativos (noticias malas) en el precio del petróleo tendrán un impacto diferente, no sólo en la volatilidad de corto plazo, sino también en la volatilidad de largo plazo que los choques positivos (noticias buenas) de la misma magnitud.

En consecuencia, el modelo CGARCH se puede extender para capturar los efectos de apalancamiento, agregando parámetros de asimetría a las ecuaciones de las varianzas de corto y largo plazos de la siguiente manera:

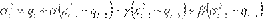(4)

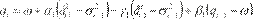(5)

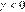
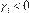
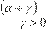
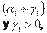
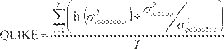
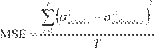
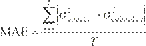donde los parámetros y miden los efectos de asimetría, cuyas propiedades son similares al componente EGARCH de Nelson (1991). Para los valores de y las implicaciones económicas significan que la presencia de noticias malas tendrán un mayor impacto en las volatilidades de corto y largo que las noticias buenas de la misma magnitud, por lo que el efecto total temporal y de largo plazo será de y

. Mientras que para los valores de

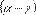las volatilidades de corto y largo plazos serán afectadas por los coeficientes y

, respectivamente. Por otra parte, dado el comportamiento no-normal en los rendimientos

(8)

(9)

(7)

de los petróleos nacionales, se asume que las innovaciones siguen una distribución de Laplace, la cual se puede definir como

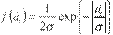(6)

Donde el parámetro de forma es igual a 1.

5.2 Medidas de evaluación predictiva

Existen diferentes criterios para la evaluación predictiva de los modelos de volatilidad, entre las medidas más comunes se encuentran las funciones de pérdidas. Para el análisis de la volatilidad fuera de muestra utilizamos los estadísticos QLIKE, error cuadrado medio (MSE) y error absoluto medio (MAE).7

Las funciones de pérdidas asociadas a la volatilidad condicional se definen como

7 Ante la presencia de ruido en la volatilidad actual, Patton (2011) demostró analíticamente que las funciones de pérdidas más robustas en la minimización del error de predicción son el error cuadrado medio (MSE) y el QLIKE.

Donde es el número de predicciones fuera de la muestra, 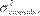y 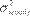representan las varianzas estimada y actual para el día .

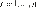Las funciones de pérdidas permiten clasificar los modelos de volatilidad con base en la exactitud de la predicción fuera de la muestra. Sin embargo, la capacidad de predicción óptima entre dos modelos de volatilidad no tiene una validación estadística a través de pruebas robustas. Para solucionar este problema, Diebold y Mariano (1995) desarrollaron una prueba estadística que permite comparar dos modelos de volatilidad usando dos conjuntos de errores de predicción 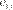y para . La diferencia entre los errores de predicción de dos modelos de volatilidad puede expresarse como

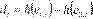(10)

Donde 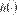es una función asociada a cada una de las funciones de pérdidas.

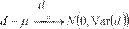
La media muestral de la diferencia entre los errores de predicción, se distribuye asintóticamente como ; es decir,

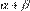
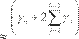(11)

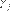
Donde es la -ésima covarianza de 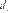, cuyo valor estimado es igual a

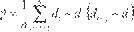(12)

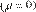Bajo la hipótesis nula de predicción óptima idéntica o media cero . El estadístico de la prueba de Diebold y Mariano (1995) puede expresarse como

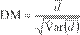(13)

Donde 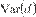es un estimador consistente de la varianza asintótica 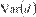y DM sigue una distribución normal estándar bajo la hipótesis nula, la cual se rechaza cuando el valor del estadístico es negativo y significativo.

6. Evidencia empírica

6.1 Estimación de los modelos de volatilidad dentro de la muestra

En esta sección se reportan los resultados de los parámetros estimados de la media condicional y varianza condicional de los modelos GARCH, EGARCH, GARCH-GJR, APARCH y CGARCH

y algunas pruebas de diagnóstico sobre los residuales estandarizados simples y cuadrados. Los parámetros de los modelos de volatilidad son estimados dentro de la muestra utilizando los rendimientos diarios del petróleo Maya e Istmo del 3 de enero de 1989 al 31 de diciembre de 2007 y el método de cuasi-máxima verosimilitud que proporciona errores estándar más robustos, asumiendo que los residuales siguen una distribución normal y distribución de Laplace.

Los resultados de los parámetros estimados de las seis estructuras GARCH y sus errores estándar son reportados en los Cuadros 3 y 4, respectivamente. Analizando los parámetros estimados de la especificación de la media condicional del petróleo Maya se puede observar que todos los estimadores son estadísticamente significativos para los diferentes niveles, excepto para los modelos GARCH (1,1), EGARCH (1,1) y ACGARCH (1,1) con innovaciones normales. En cambio para el petróleo Istmo, la significancia del coeficiente del proceso de la media condicional es sólo alcanzada para las aproximaciones basadas en la distribución de Laplace a un nivel de 1%. En cuanto a los parámetros del proceso de la varianza condicional, todos los modelos GARCH capturan exitosamente los patrones dinámicos de la volatilidad dinámica ampliamente documentado en la literatura empírica, dado que sus estimadores son positivos y estadísticamente significativos en los niveles convencionales, excepto para el modelo CGARCH con innovaciones de Laplace del petróleo Istmo. Por su parte, los valores estimados del coeficiente de persistencia oscilan entre 0.7926-0.9972 para el petróleo Maya y entre 0.6370-0.9982 para el petróleo Istmo, que implica la presencia de un alto grado de persistencia en la volatilidad condicional en ambas series. Este hecho es sustentado por los parámetros estimados de 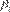en el modelo CGARCH (1,1), que confirman que el componente de la volatilidad de largo plazo es más persistente que el componente de la volatilidad de corto plazo; es decir, 0.9273 contra 0.7926 (normal) y 0.9430 contra 0.8015 para el Maya (Laplace), en tanto que para el Istmo 0.9210 contra 0.6370 (normal) y 0.9300 contra 0.6737 (Laplace). No obstante, estos resultados no son sustentados por el modelo CGARCH asimétrico, en donde el componente de la volatilidad de corto plazo es más persistente que el componente de largo plazo. Este hecho puede ser atribuido en parte a los resultados mixtos de los efectos de apalancamiento temporales y de largo plazo.

Cuadro 3. Resultados de los modelos estimados del petróleo Maya

	Distribución Normal						Distribución de Laplace
	GARCH	EGARCH	GJR	APARCH	CGARCH	ACGARCH	GARCH	EGARCH	GJR	APARCH	CGARCH	ACGARCH
μ	0.0432	0.0304	0.0511***	0.0647*	0.0631**	0.0431	0.0759*	0.0728*	0.0743*	0.0732*	0.0772*	0.0745*
	(0.0282)	(0.0286)	(0.0303)	(0.0299)	(0.0285)	(0.0285)	(0.0223)	(0.0221)	(0.0224)	(0.0222)	(0.0223)	(0.0221)
ω	0.0844*	-0.1027*	0.0862*	0.0434*	0.0173*	0.0182*	0.1027*	-0.0830*	0.1041*	0.0376*	0.0177*	0.0131
	(0.0079)	(0.0036)	(0.0081)	(0.0057)	(0.0088)	(0.0040)	(0.0233)	(0.0103)	(0.0233)	(0.0118)	(0.0150)	(0.0083)
α	0.0819*	0.1702*	0.0777*	0.0811*	0.0529*	0.1262*	0.0749*	0.1516*	0.0639*	0.0834*	0.0657*	0.1072*
	(0.0029)	(0.0059)	(0.0037)	(0.0039)	(0.0016)	(0.0099)	(0.0089)	(0.0154)	(0.0109)	(0.0092)	(0.0257)	(0.0226)
β	0.9115*	0.9871*	0.9099*	0.9161*	0.7397*	0.9942*	0.9163*	0.9855*	0.9162*	0.9135*	0.7378*	0.9920*
	(0.0034)	(0.0011)	(0.0035)	(0.0033)	(0.1016)	(0.0009)	(0.0091)	(0.0032)	(0.0091)	(0.0081)	(0.1567)	(0.0029)
α1					0.0542*	0.1264*					0.0369***	0.1150*
					(0.0158)	(0.0196)					(0.0199)	(0.0369)
β1					0.9273*	0.7763*					0.9430*	0.7991*
					(0.0102)	(0.0430)					(0.0158)	(0.1083)
γ		-0.0952*	0.0136**	-0.0819*		-0.1953*		-0.1389*	0.0212	-0.1322**		-0.1936**
		(0.0226)	(0.0061)	(0.0207)		(0.0430)		(0.0644)	(0.0145)	(0.0621)		(0.1114)
γ1						0.2090*						-0.0040
						(0.0759)						(0.1765)
δ				1.3773*						1.1531*
				(0.0801)						(0.1751)
α+β	0.9935	0.9871	0.9876	0.9972	0.7916	0.9942	0.9913	0.9855	0.9801	0.9969	0.8015	0.9920
Log(L)	-11387	-11383	-11385	-11379	-11384	-11368	-11073	-11062	-11072	-11063	-11070	-11056
AIC	2.2782	2.2777	2.2781	2.2771	2.2780	2.2753	2.2154	2.2134	2.2154	2.2138	2.2153	2.2127
BIC	2.2808	2.2810	2.2814	2.2810	2.2819	2.2805	2.2180	2.2166	2.2186	2.2177	2.2192	2.2179
Q(12)	10.59	10.86	10.17	10.57	10.71	10.91	10.25	10.18	9.54	10.32	10.37	10.39
	[0.5646]	[0.5409]	[0.6007]	[0.5657]	[0.5542]	[0.5369]	[0.5938]	[0.5999]	[0.6563]	[0.5875]	[0.5835]	[0.5820]
Q2(12)	18.59	19.21	18.56	18.93	18.16	15.15	19.78	21.37	19.18	20.54	18.27	17.49
	[0.0989]	[0.0837]	[0.0998]	[0.0901]	[0.1109]	[0.2315]	[0.0713]	[0.0451]	[0.0841]	[0.0575]	[0.1079]	[0.1322]

Nota: Log (L) es el valor máximo de la función de verosimilitud logarítmica. AIC y BIC representan los criterios de información de Akaike y Schwarz, respectivamente. Q (12) y Q2(12) indican los estadísticos de la prueba de Ljung-Box para los residuales simples y cuadrados con 12 Rezagos y valores-p entre corchetes cuadrados. Los términos *, ** y *** indican significancia a niveles del 1%, 5% y 10%, respectivamente.

Los errores estándar se reportan entre paréntesis.

Considerando el coeficiente del impacto asimétrico de las noticias, todos los parámetros estimados

, con la excepción del modelo GJR (1,1) con distribución de Laplace para las innovaciones del petróleo Maya, son significativamente diferentes de cero a niveles de 1% y 5%, respectivamente. Este hallazgo indica que los choques negativos tienen un mayor impacto en la volatilidad condicional que los choques positivos de la misma magnitud. En el caso del Istmo, el coeficiente asociado con la característica de volatilidad asimétrica; sin embargo, no es estadísticamente significativo diferente de cero a cualquier nivel y bajo los diferentes supuestos distribucionales, con la excepción del modelo CGARCH (1,1) asimétrico basado en la distribución normal, aunque con resultados mixtos. El signo y la significancia del parámetro de asimetría en el modelo CGARCH (1,1) asimétrico muestran fuerte evidencia de efectos de apalancamiento en los rendimientos del petróleo mexicano, cuyo impacto negativo incrementa en forma dramática el grado de persistencia en el componente de la volatilidad de corto plazo, pero que tiende a disminuir significativamente en el largo plazo ante la presencia de efectos asimétricos con signo positivo.

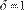
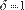Por su parte, los coeficientes del término de potencia del modelo APARCH (1,1) son significativamente diferentes de cero con valores entre 1.3737-1.1531 para el petróleo Maya y entre 1.5878-1.1459 para el petróleo Istmo bajo innovaciones normales y de Laplace, respectivamente. Para ambos tipos de petróleo y bajo la distribución de Laplace es imposible rechazar la hipótesis nula de que a un nivel de significancia de 5%, indicando que el modelo de la desviación estándar condicional es más apropiado para la modelación del proceso de la volatilidad. No obstante, la hipótesis nula de

es fácilmente rechazada para el modelo APARCH

(1,1) con innovaciones normales, pero no para

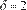. Este hallazgo señala que la volatilidad de los rendimientos del petróleo Istmo es mejor

modelada a través de la varianza condicional. En tanto que para la serie de los rendimientos del petróleo Maya, ambas hipótesis nulas son rechazadas para el modelo APARCH (1,1) con innovaciones normales condicionales.

Para el proceso de la selección del modelo de volatilidad se utiliza la función de verosimilitud, los criterios AIC y BIC. En términos absolutos, los pequeños valores de los indicadores antes mencionados sustentan que los modelos CGARCH (1,1) asimétrico con innovaciones normales condicionales son más flexibles para explicar las características de la volatilidad condicional en ambos tipos de petróleo, seguido por el modelo APARCH (1,1) y CGARCH (1,1) a pesar de que los modelos GARCH estándar y GJR (1,1) reportan criterios de información de Schwarz más bajos; es decir, 2.2222 y 2.2230 contra 2.2248 para el petróleo Istmo. Este hecho se atribuye a que el BIC penaliza a los modelos de volatilidad cuando se estiman parámetros adicionales. Por su parte, los modelos EGARCH (1,1) y ACGARCH (1,1) con innovaciones de Laplace muestran resultados superiores al resto de las especificaciones para describir eficientemente características de la heteroscedasticidad condicional, la volatilidad en aglomeraciones, la persistencia de los choques e incluso los efectos de apalancamiento tanto temporales como de largo en las series del petróleo.

Cuadro 4. Resultados de los modelos estimados del petróleo Istmo

	Distribución Normal						Distribución de Laplace
	GARCH	EGARCH	GJR	APARCH	CGARCH	ACGARCH	GARCH	EGARCH	GJR	APARCH	CGARCH	ACGARCH
μ	0.0270	0.0217	0.0342	0.0403	0.0304	0.0219	0.0630*	0.0594*	0.0623*	0.0601*	0.0648*	0.0603*
	(0.0283)	(0.0276)	(0.0297)	(0.0299)	(0.0284)	(0.0285)	(0.0222)	(0.0219)	(0.0222)	(0.0221)	(0.0222)	(0.0220)
ω	0.1147*	-0.0904*	0.1138*	0.0789*	0.0410***	0.0095*	0.1091*	-0.0732*	0.1117*	0.0440*	0.0332	0.0083
	(0.0116)	(0.0043)	(0.0114)	(0.0116)	(0.0220)	(0.0033)	(0.0272)	(0.0110)	(0.0275)	(0.0143)	(0.0531)	(0.0076)
α	0.0742*	0.1703*	0.0703*	0.0850*	0.0445*	0.1071*	0.0690*	0.1427*	0.0638*	0.0771*	0.0333	0.0952*
	(0.0035)	(0.0075)	(0.0042)	(0.0050)	(0.0147)	(0.0134)	(0.0095)	(0.0173)	(0.0124)	(0.0100)	(0.0313)	(0.0268)
β	0.9088*	0.9789*	0.9090*	0.9117*	0.5924*	0.9874*	0.9200*	0.9835*	0.9192*	0.9211*	0.6454	0.9910*
	(0.0049)	(0.0020)	(0.0049)	(0.0049)	(0.1741)	(0.0021)	(0.0106)	(0.0043)	(0.0107)	(0.0096)	(0.4913)	(0.0039)
α1					0.0555*	0.0914*					0.0541**	0.0864
					(0.0111)	(0.0180)					(0.0251)	(0.0377)
β1					0.9210*	0.8472*					0.9300*	0.8499*
					(0.0095)	(0.0452)					(0.0184)	(0.1172)
γ		-0.0372	0.0078	-0.0289		-0.2439*		-0.0967	0.0106	-0.0991		-0.1124
		(0.0260)	(0.0063)	(0.0236)		(0.0696)		(0.0765)	(0.0156)	(0.0742)		(0.1350)
γ1						0.4761*						-0.0739
						(0.1287)						(0.2500)
δ				1.5878*						1.1459*
				(0.1021)						(0.1966)
α+β	0.9831	0.9789	0.9793	.9968	0.6370	0.9874	0.9890	0.9835	0.9831	0.9982	0.6787	0.9910
Log(L)	-11094	-11100	-11094	-11091	-11092	-11090	-10887	-10878	-10887	-10879	-10886	-10877
AIC	2.2196	2.2210	2.2198	2.2194	2.2196	2.2196	2.1783	2.1767	2.1784	2.1770	2.1785	2.1769
BIC	2.2222	2.2243	2.2230	2.2233	2.2235	2.2248	2.1809	2.1800	2.1817	2.1809	2.1824	2.1821
Q(12)	6.39	6.83	6.34	6.51	6.24	6.51	6.46	7.06	6.43	6.87	6.28	6.69
	[0.8949]	[0.8684]	[0.8980]	[0.8881]	[0.9033]	[0.8881]	[0.8914]	[0.8536]	[0.8929]	[0.8660]	[0.9011]	[0.8776]
Q2(12)	25.93	26.66	25.81	26.36	27.50	22.61	24.67	25.61	24.59	24.80	24.95	22.71
	[0.0710]	[0.0580]	[0.0812]	[0.0951]	[0.1163]	[0.1312]	[0.0642]	[0.0904]	[0.0764]	[0.0705]	[0.1582]	[0.1303]

Nota: Log (L) es el valor máximo de la función de verosimilitud logarítmica. AIC y BIC representan los criterios de información de Akaike y Schwarz, respectivamente. Q (12) y Q2(12) indican los estadísticos de la prueba de Ljung-Box para los residuales simples y cuadrados con 12 rezagos y valores-p entre corchetes cuadrados. Los términos *, ** y *** indican significancia a niveles de 1%, 5% y 10%, respectivamente. Los errores estándar se reportan entre paréntesis.

Asimismo, el diagnóstico de los residuales estandarizados simples y cuadrados a través de la prueba de Ljung-Box con 12 rezagos señala que todos los modelos GARCH muestran suficiente evidencia a favor de la especificación correcta de la media condicional para explicar apropiadamente el comportamiento de los rendimientos del petróleo bajo cualquier supuesto distribucional. Esto obedece a los altos valores-p que rechazan la presencia de correlación serial en los residuales estandarizados simples a un nivel de significancia del 5%. En el

caso de los residuales estandarizados cuadrados, la significancia de los estadísticos de la prueba de Ljung-Box confirman la capacidad de los modelos de dos componentes para corregir la correlación serial en la ecuación de la varianza condicional de los rendimientos del petróleo Maya e Istmo, y para cualquier distribución de innovaciones. Este hecho indica que no existe evidencia estadísticamente significativa de error de especificación en los modelos CGARCH para describir la heteroscedasticidad exhibida en el mercado del petróleo mexicano.

6.2 Evaluación de la predicción óptima de la volatilidad fuera de la muestra

Para evaluar la precisión y eficiencia de los modelo GARCH fuera de la muestra, utilizamos el periodo del 2 de enero de 2008 al 31 de diciembre de 2012 para reestimar la varianza condicional a través de una ventana móvil, removiendo la observación más remota y agregando la observación más reciente al periodo muestral, cuya predicción se compara con la varianza actual medida por la variable proxy de los rendimientos cuadrados.8 El proceso es repetido hasta obtener el error de predicción del 31 de diciembre de 2012 para cada horizonte de tiempo. De esta manera, el tamaño de la muestra se mantiene fijo durante la reestimación de los modelos de volatilidad y las predicciones fuera de la muestra no se traslapan.

El Cuadro 5 reporta los valores de las funciones de pérdidas y los estadísticos de Diebold-Mariano para los horizontes predicción de 1, 5 y 20 días. Los modelos benchmark son seleccionados tomando como referencia la clasificación más alta derivado del valor más pequeño de los diferentes criterios QLIKE, MSE y MAE. En este sentido, los rendimientos del petróleo Maya prefieren el modelo CGARCH (1,1) asimétrico con innovaciones normales para la predicción de la volatilidad a través de los criterios QLIKE y MSE, mientras que el criterio MAE apoya al mismo modelo de volatilidad asimétrico, pero basado en la distribución de Laplace para el horizonte de predicción 1 y 20 días, respectivamente.

Los resultados bajo los diferentes horizontes de predicción muestran evidencia empírica mixta para las innovaciones del petróleo Istmo, por ejemplo, el modelo CGARCH (1,1) asimétrico con distribución normal alcanza el valor más pequeño en los errores de predicción bajo los diferentes horizontes y criterios QLIKE y MAE, excepto para

8 Este medida proxy es la más común utilizada en la literatura porque si el modelo estimado está correctamente especificado, el error cuadrado representa un estimador insesgado de la varianza diaria.

horizonte de 20 días en donde el modelo CGARCH con innovaciones normales muestra superior capacidad a todos los modelos alternativos para predecir la volatilidad fuera de la muestra. Para los horizontes de 1 y 5 días, el modelo CGARCH (1,1) con innovaciones de Laplace distribuidas proporciona el error de predicción más pequeño de acuerdo con el criterio MSE, resaltando la importancia de la distribución de colas pesadas para capturar la leptocurtosis en las innovaciones de los rendimientos del petróleo crudo. En tanto que el modelo CGARCH (1,1) con distribución normal es notablemente superior a los modelos alternativos para el horizonte de predicción de 20 días.

La validación estadística del desempeño de los modelos benchmark sobre los modelos alternativos aunado a la importancia de los supuestos distribucionales se determina a través de la prueba estadística de Diebold-Mariano (DM). Para los rendimientos del crudo Maya y bajo los criterios QLIKE y MSE, los valores negativos del estadístico DM rechazan fuertemente la hipótesis nula de capacidad predictiva idéntica en los diferentes horizontes de predicción, mostrando el poder predictivo del modelo CGARCH (1,1) asimétrico con innovaciones normales con respecto a los modelos de volatilidad comparados, con la excepción del horizonte de 20 días. Asimismo, bajo la distribución de Laplace y el criterio MAE el modelo CGARCH (1,1) asimétrico continúa mostrando superior capacidad predictiva sobre los modelos de volatilidad en los horizontes de predicción de 1 y 20 días. De hecho, la capacidad de predicción óptima igual se mantiene sólo con respecto a los modelos CGARCH (1,1) asimétrico y EGARCH (1,1) con innovaciones normales.

Para los rendimientos del petróleo Istmo y los tres horizontes de predicción, el modelo CGARCH asimétrico basado en la distribución normal parecen ser las especificación más apropiada para predecir la volatilidad fuera de la muestra bajo

los criterios QLIKE y MAE, porque sólo en 7 casos el modelo benchmark presentan el mismo poder predictivo con respecto a los modelos predictivos comparados (GARCH estándar, GJR, APARCH, CGARCH basado en la distribución normal y GJR y CGARCH basado en la distribución de Laplace). En tanto que bajo el criterio MSE el poder predictivo superior del modelo CGARCH con innovaciones de Laplace es sólo alcanzado sobre los modelos EGARCH y APARCH bajo los diferentes supuestos distribucionales y horizonte de 1 día. No obstante, los resultados del estadístico DM señalan que el modelo CGARCH con innovaciones normales proporciona predicción óptima idéntica bajo el criterio SME y horizonte de 20 días, aunque cabe resaltar que su desempeño sólo es superior a 5 modelos de volatilidad bajo el criterio MAE.

Los resultados del presente estudio muestran la importancia de considerar los efectos de apalancamiento y la persistencia en el proceso de la predicción de la volatilidad condicional, porque a pesar de que la presencia de los efectos de asimetría de largo plazo reducen el grado de persistencia en el componente de la volatilidad condicional de largo; sin embargo, sus consecuencias no distorsionan el poder predictivo del modelo CGARCH asimétrico, considerado empíricamente como el mejor modelo en términos del poder predictivo de la volatilidad condicional en los rendimientos de los precios del petróleo, debido al hecho de que en 14 de 18 casos (77.78%) es seleccionado como modelo benchmark para predecir la volatilidad fuera de la muestra y bajo las tres funciones de pérdidas. Por otra parte, la relajación de los efectos de apalancamiento en el modelo CGARCH puede alcanzar aún el poder predictivo superior en algunos casos, en particular para la serie de los rendimientos del petróleo Istmo.

7. Conclusiones

Con el propósito de capturar los efectos asimétricos temporales y permanentes de los precios del petróleo mexicano de exportación, así como predecir su volatilidad condicional este

trabajo aplica, con propósitos comparativos, las distribuciones normal y de Laplace respecto a cinco modelos de volatilidad que incluyen a los modelos GARCH estándar, EGARCH, GJR, APARCH y CGARCH. La muestra comprende los precios diarios de los petróleos Maya e Istmo para el período 1989 a 2012. La evidencia empírica indica que las series de los rendimientos de los precios del petróleo, en particular el crudo Maya, presentan efectos de apalancamiento permanentes con signo negativo que incrementan la volatilidad de corto plazo, mientras que el componente de la volatilidad de largo plazo no es compensada por los choques positivos. Los resultados fuera de la muestra basados en la prueba estadística de Diebold-Mariano (1995) identifican empíricamente al modelo CGARCH asimétrico como el mejor en términos de poder predictivo que los modelos de volatilidad comparados, atribuido a que en 14 de 18 casos es seleccionado como modelo benchmark para predecir la volatilidad fuera de la muestra y bajo las tres funciones de pérdidas. El alcance del modelo CGARCH en cierta medida es limitado para capturar la característica de asimetría; sin embargo su poder predictivo superior aún se mantiene en algunos casos, en particular en los rendimientos del petróleo Istmo. De esta manera, los hallazgos empíricos proporciona información más completa de la dinámica de la estructura de la volatilidad en periodos de crisis financieras y episodios de tensiones geopolíticas a nivel internacional y del riesgo de los mercados de energía de baja calidad y alto contenido de azufre a consumidores, inversionistas, reguladores y gobiernos, quienes utilizan las predicciones de la volatilidad para mejorar la determinación de los requerimientos de capital a través de las medidas valor en riesgo, el diseño de estrategias de cobertura óptima y la valuación de productos derivados sobre el activo subyacente del petróleo mexicano.

En cuanto a la política energética y de desarrollo de los países exportadores de petróleo una apropiada estimación de los efectos asimétricos negativos en

la volatilidad de corto plazo puede contribuir a una mejor formulación de políticas de cobertura para reducir la presión e incertidumbre de la volatilidad de los precios del petróleo en los mercados internacionales. En el caso de México un eficiente

control de la volatilidad petrolera puede redundar en una mejor política fiscal y mantenimiento de la estabilidad en la economía doméstica que permitan enfocar la política económica hacia un desarrollo sostenido.

Cuadro 4. Resultados de los estadísticos y pruebas de Diebold-Mariano para la predicción óptima de la varianza condicional.

Panel A: Petróleo Maya
	1 día						5 días						20 días
	QLIKE	DM	MSE	DM	MAE	DM	QLIKE	DM	MSE	DM	MAE	DM	QLIKE	DM	MSE	DM	MAE	DM
GARCH-N	2.638(9)	-2.56*	24.573(10)	-2.66*	8.788(6)	-4.89*	2.658(8)	-3.98*	15.099(11)	-1.71**	7.698(8)	-2.02**	2.742(6)	-1.85**	20.448(7)	-0.94	8.876(7)	-2.62*
EGARCH-N	2.642(10)	-3.48*	24.483(7)	-2.73*	8.848(8)	-4.81*	2.655(7)	-5.17*	14.670(2)	-1.53	7.551(4)	-2.39*	2.705(3)	-0.10	20.198(3)	-0.82	8.745(2)	-1.40
GJR-N	2.633(8)	-2.62*	24.426(6)	-2.30**	8.741(5)	-4.99*	2.647(5)	-3.65*	15.052(8)	-1.82**	7.634(6)	-1.74**	2.762(10)	-3.06*	20.608(8)	-1.09	9.199(9)	-2.42*
APARCH-N	2.320(5)	-5.56*	24.686(12)	-3.08*	8.915(9)	-3.62*	2.654(6)	-4.91*	14.701(3)	-1.37	7.588(5)	-2.52*	2.759(9)	-3.63*	20.678(10)	-1.22	9.307(11)	-2.15**
CGARCH-N	2.598(4)	-4.18*	24.349(4)	-1.77**	8.590(3)	-1.69**	2.624(3)	-1.56	14.843(4)	-1.47	7.518(3)	-1.42	2.734(5)	-1.68**	20.404(6)	-0.89	8.787(4)	-2.07**
ACGARCH-N	2.560(1)	-	23.909(1)	-	8.561(2)	-0.52	2.605(1)	-	13.913(1)	-	7.421(1)	-	2.702(1)	-	19.210(1)	-	8.848(5)	-2.02**
GARCH-L	2.630(7)	-8.31*	24.508(8)	-2.65*	8.909(10)	-7.69*	2.683(12)	-5.42*	15.281(12)	-1.84**	7.899(11)	-1.84**	2.757(8)	-2.46*	20.611(9)	-0.98	9.038(8)	-3.31*
EGARCH-L	2.650(12)	-9.11*	24.547(9)	-2.99*	8.975(11)	-7.25*	2.676(10)	-7.46*	14.983(6)	-1.72**	7.759(10)	-3.37*	2.779(11)	-4.28*	20.777(11)	-1.07	9.279(10)	-2.92*
GJR-L	2.626(6)	-9.07*	24.415(5)	-2.53*	8.845(7)	-8.01*	2.666(9)	-5.31*	15.084(9)	-1.87**	7.749(9)	-2.25**	2.748(7)	-2.35*	20.397(5)	-0.90	8.872(6)	-3.33*
APARCH-L	2.643(11)	-8.54*	24.639(11)	-3.67*	9.092(12)	-5.05*	2.678(11)	-7.71*	14.983(7)	-1.93**	7.810(12)	-3.72*	2.789(12)	-5.30*	21.085(12)	-1.31	9.656(12)	-2.25**
CGARCH-L	2.584(3)	-2.61*	24.226(3)	-1.24	8.628(4)	-3.81*	2.646(4)	-3.00*	15.098(10)	-1.86**	7.681(7)	-1.85**	2.713(4)	-0.43	20.241(4)	-0.81	8.785(3)	-1.73**
ACGARCH-L	2.572(2)	-1.88**	24.226(2)	-1.04	8.514(1)	-	2.623(2)	-1.49	14.907(5)	-1.38	7.493(5)	-1.10	2.702(2)	-0.01	20.058(2)	-0.71	8.575(1)	-

Panel B: Petróleo Istmo
	1 día						5 días						20 días
	QLIKE	DM	MSE	DM	MAE	DM	QLIKE	DM	MSE	DM	MAE	DM	QLIKE	DM	MSE	DM	MAE	DM
GARCH-N	2.707(2)	-1.64	25.515(5)	-1.58	9.414(3)	-2.97*	2.681(4)	-3.40*	27.323(5)	-1.18	9.170(5)	-2.29**	2.818(8)	-2.71*	50.516(5)	-1.08	14.067(5)	-1.22
EGARCH-N	2.730(10)	-5.11*	26.040(12)	-1.79**	9.348(2)	-4.81*	2.699(10)	-4.60*	28.670(12)	-1.12	9.171(6)	-3.17*	2.819(9)	-3.74*	52.105(11)	-1.03	14.133(6)	-1.28
GJR-N	2.709(4)	-2.20*	25.519(6)	-0.86	9.479(5)	-3.40*	2.682(5)	-3.71*	27.950(7)	-1.14	9.186(7)	-2.01**	2.803(6)	-1.16	50.994(8)	-1.06	14.165(7)	-1.36
APARCH-N	2.725(8)	-3.62*	25.824(10)	-1.95**	9.494(7)	-5.45*	2.689(6)	-4.50*	28.092(9)	-0.98	9.160(4)	-2.64**	2.768(3)	-0.40	50.166(3)	-1.03	13.959(4)	-1.37
CGARCH-N	2.708(3)	-1.80**	25.464(2)	-0.76	9.421(4)	-3.36*	2.656(2)	-1.67**	27.217(2)	-0.93	8.992(2)	-1.48	2.774(4)	-0.22	49.309(1)	-	13.718(1)	-
ACGARCH-N	2.688(1)	-	25.789(8)	-1.41	9.159(1)	-	2.637(1)	-	27.624(3)	-0.94	8.791(1)	-	2.763(1)	-	50.467(4)	-0.99	13.750(2)	-0.19
GARCH-L	2.718(6)	-2.66*	25.499(3)	-1.34	9.569(9)	-4.46*	2.695(8)	-4.46*	27.770(4)	-1.21	9.305(11)	-2.97*	2.804(7)	-3.16*	50.625(6)	-1.07	14.297(8)	-2.06**
EGARCH-L	2.740(12)	-6.94*	26.017(11)	-1.82**	9.484(6)	-7.84*	2.711(11)	-5.58*	28.618(11)	-1.13	9.289(9)	-4.28*	2.848(12)	-2.38*	52.286(12)	-1.04	14.449(10)	-1.87**
GJR-L	2.719(7)	-3.24*	25.507(4)	-0.67	9.616(11)	-4.59*	2.694(7)	-4.74*	27.906(6)	-1.15	9.300(10)	-2.53*	2.801(5)	-1.56	50.958(7)	-1.06	14.366(9)	-1.98**
APARCH-L	2.731(11)	-4.53*	25.815(9)	-2.03**	9.596(10)	-6.63*	2.698(9)	-5.33*	28.060(8)	-0.97	9.256(8)	-3.17*	2.835(10)	-3.64*	51.491(9)	-1.05	14.469(11)	-2.19**
CGARCH-L	2.714(5)	-2.43*	25.459(1)	-	9.499(8)	-4.21*	2.664(3)	-2.26**	27.188(1)	-	9.060(3)	-1.91*	2.765(2)	-0.13	49.529(2)	-0.98	13.932(3)	-1.50
ACGARCH-L	2.724(9)	-4.69*	25.672(7)	-1.47	9.706(12)	-6.98*	2.711(12)	-5.46*	28.571(10)	-1.29	9.791(12)	-4.12*	2.842(11)	-2.84*	51.910(10)	-1.07	14.561(12)	-1.94**

Nota: Los valores en negritas indican los modelos con clasificación más alta considerando los valores más pequeños de los diferentes criterios QLIKE, MSE y MAE. DM indica el valor de la prueba de

Diebold-Mariano para validar la hipótesis nula de que la predicción óptima del modelo benchmark es idéntica a la de los modelos alternativos. *, ** indican el rechazo de la hipótesis nula a un nivel de significancia del 1% y 5%.

Referencias

Agnolucci, P. (2009). Volatility in crude oil futures: A comparison of the predictive ability of GARCH and implied volatility models. Energy Economics, vol. 31, num. 2, pp. 316-321.

Baillie, R.T., Bollerslev, T., y Mikkelsen, H.O. (1996). Fractionally integrated generalised autoregressive conditional heteroskedasticity. Journal of Econometrics, vol. 74, num. 1, pp. 3-30.

Baker, H.K., Rahman, A., and Saadi, S. (2008) The day-of-the-week and conditional volatility: sensitivity of the distributional assumptions. Review of Financial Economics, vol. 17, num. 4, pp. 280-

297.

Bibby, B.M., and Sorensen, M. (2003). Hyperbolic processes in finance, en: Rachev, S. T. (editor), Handbook of Heavy Tailed Distributions in Finance. Elsevier Science, Amsterdam.

Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, vol. 31, num. 3, pp. 307-327.

Chang, K.L. (2012). Volatility regimes, asymmetric basis effects and forecasting performance: an empirical investigation of the WTI crude oil futures market. Energy Economics, vol. 34, num. 1, pp. 294-306.

Cheong, C.W. (2009). Modeling and forecasting crude oil markets using ARCH-type models. Energy Policy, vol. 36, num. 6, pp.2346-2355.

Christoffersen, P, Jacobs, K., and Wang, Y. (2006). Option valuation with long-run and short-run volatility components. Unpublished Working Paper. McGill University.

Diebold, F.X., and Mariano, R.Ss (1995). Comparing predictive accuracy. Journal of Business & Economic Statistics, vol. 13, num. 3, pp. 253-263.

Ding Z, Granger CW, Engle RF (1993). A long memory property of stock market returns and a new model. Journal of Empirical Finance, vol. 1, num. 1, pp. 83-106.

Engle, R.T. (1982). Autoregressive conditional heteroskedasticity with estimates of variance of United Kingdom inflation. Econometrics, vol. 50, num. 4, pp. 987-1007.

Engle, R,F., and Lee, G.G. (1999). A permanent and transitory component model of stock return volatility, en: Engle, R. F., and White, H. (eds.). Cointegration, casuality and forecasting: A Festschrift in Honor of Clive W. J. Granger. Oxford University Press, Oxford, pp. 475-497.

Federer, J.P. (1996). Oil price volatility and the macroeconomic. Journal of Macroeconomics, vol. 18, num. 1, pp. 1-26.

Granger, C.W.J., and Ding, Z. (1995). Some properties of absolute return, an alternative measure of risk. Annales D’économie et the statistique, vol. 40 (Oct-Dec), pp. 67-91.

Hamilton, J.D., and Herrera, A.M. (2004). Oil shocks and aggregate macroeconomic behavior: the role of monetary policy. Journal of Money, Credit and Banking, vol. 36, num. 2, pp. 751-782.

Hou, A., y Suardi, S. (2012). A nonparametric GARCH model of crude oil price return volatility. Energy Economics, vol. 34, num. 2, pp. 616-626.

Kang, S.H., Kang, S.M., y Yoon, S.M. (2009).

Forecasting volatility of crude oil markets. Energy Economics, vol. 31, num. 1, pp. 119-125.

Kilian, L. (2009). Not all oil price shocks are alike: disentangling demand and supply shocks in the crude oil market. American Economic Review, vol. 99, num. 3, pp. 1053-1069.

Marzo, M., y Zagaglia, P. (2010). Volatility forecasting for crude oil futures. Applied Economics Letters, vol. 17, num. 16, pp. 1587-1599.

Mittnik, S., Paolella, M.S., y Rachev, S.T. (1998). Unconditional and conditional distributional models for Nikkei index. Asia-Pacific Financial Markets, vol. 5, num. 2, pp. 99-128.

Narayan, P.K., y Narayan, S. (2007). Modelling oil price volatility. Energy Policy, vol. 35, num. 12, pp. 6549-6553.

Nelson, D. (1991). Conditional heteroskedasticity in asset returns: a new approach. Econometrica, vol. 59, num. 2, pp. 347-370.

Patton, A.J. (2011). Volatility forecast comparison using imperfect volatility proxies. Journal of Econometrics, vol. 160, num. 1, pp. 246-256.

Pemex, Mexico’s Energy Reform & Pemex as a State Productive Enterprise. Pemex 2014. www. pemex.co.

PricewaterhouseCoopers, The World in 2050. The BRICs and Beyond: Prospects, Challenges and Opportunities., 2013

Sadorsky, P. (2006). Modeling and forecasting petroleum futures volatility. Energy Economics, vol. 28, num. 4, pp. 467-488.

Salisu, A.A., y Fasanya, I.O. (2012). Comparative performance of volatility models for oil price. International Journal of Energy Economics and Policy, vol. 2, num. 3, pp. 167-183.

Wei, Y., Wang, Y., y Huang, D. (2010). Forecasting crude oil market volatility: further evidence using GARCH-class models. Energy Economics, vol. 32, num. 6, pp. 1477-1484.

Xu, B., y Ouenniche, J. (2012). A data envelopment analysis-based framework for the relative performance evaluation of competing crude oil price’ volatility forecasting models. Energy Economics, vol. 34, num. 2, pp. 576-583.